Kervaire Değişmezi Gizemi Çözüldü: Matematik Dünyasında Devrim Niteliğinde Bir Adım

Matematik dünyası, onlarca yıldır süregelen ve çözümü zorlu bir bilmece olan “Kervaire değişmezi” probleminin nihayet çözülmesini kutluyor. Çinli bilim insanlarının bu alanda gerçekleştirdiği çığır açan çalışma, matematik camiasında büyük bir heyecan yaratmış durumda. Hakem değerlendirme sürecinin tamamlanmasıyla birlikte, bu keşfin matematik alanında yeni ufuklar açması bekleniyor.
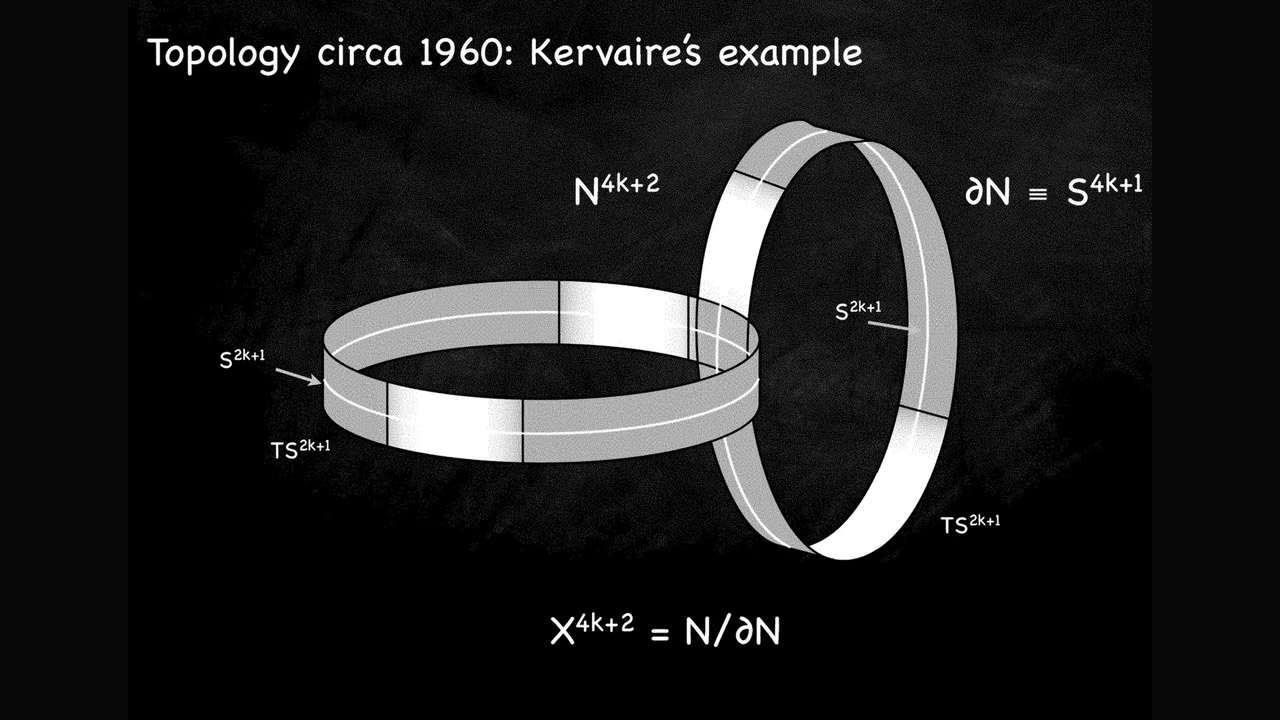
Kervaire Değişmezi Nedir?
Kervaire değişmezi, topoloji alanında önemli bir kavramdır. Basitçe ifade etmek gerekirse, bir topolojik şeklin (manifold) “cerrahi” adı verilen bir matematiksel işlemle küreye dönüştürülüp dönüştürülemeyeceğini ölçen bir fonksiyondur. Eğer dönüşüm mümkünse, fonksiyonun değeri 0 olur; aksi takdirde, değer 1 olarak belirlenir. Bu değişmezin anlaşılması ve hesaplanması, topolojik uzayların sınıflandırılması ve anlaşılması açısından kritik öneme sahiptir.
Topolojik Şekiller ve Manifoldlar
Topolojik şekiller veya manifoldlar, yerel olarak Öklid uzayına benzeyen matematiksel nesnelerdir. Örneğin, bir küre yüzeyi veya bir torus (simit şekli) birer manifold örneğidir. Bu şekillerin incelenmesi, matematiğin birçok alanında ve hatta fizikte önemli uygulamalara sahiptir.
Cerrahi İşlemi
Cerrahi işlemi, bir manifold üzerinde yapılan ve topolojik özelliklerini değiştiren bir tür matematiksel manipülasyondur. Bu işlem, manifold üzerinde belirli kesimler yaparak ve bu kesimleri farklı şekillerde birleştirerek gerçekleştirilir. Kervaire değişmezi, bu cerrahi işlemlerin sonucunda manifoldun küreye dönüştürülüp dönüştürülemeyeceğini belirlemeye yardımcı olur.
Çinli Bilim İnsanlarının Başarısı
Pekin Üniversitesi’nden Xu Zhouli, Wang Guozhen ve Lin Weinan adlı bilim insanları, Kervaire değişmezi ile ilgili 65 yıldır çözülemeyen bir sorunu çözmeyi başardılar. Bu başarı, matematik dünyasında büyük bir yankı uyandırdı ve bilim insanlarının uzun süredir devam eden çabalarının bir sonucu olarak değerlendiriliyor.
Çalışmanın Detayları
Çinli bilim insanları, Kervaire değişmezi problemini çözmek için geleneksel yöntemlere ek olarak bilgisayar sistemlerinden de yararlandılar. 126. boyutta Kervaire değişmezinin değerini belirlemek için yoğun bir çalışma yürüttüler. Bu süreçte, 105 farklı olasılığı tek tek inceleyerek ve eleyerek sonuca ulaşmayı başardılar.
126. Boyutun Önemi
Kervaire değişmezi, farklı boyutlarda farklı değerler alabilir. Bilim insanları, uzun yıllar boyunca hangi boyutlarda değişmezin değerinin 1 olduğunu bulmaya çalıştılar. Daha önce 2, 6, 14, 30 ve 62. boyutlarda değerin 1 olduğu tespit edilmişti. Çinli bilim insanlarının çalışmasıyla, 126. boyutta da değerin 1 olduğu kanıtlanmış oldu. Bu keşif, Kervaire değişmezi ile ilgili genel teorilerin geliştirilmesine katkı sağlayacak önemli bir adım olarak görülüyor.
Kervaire Değişmezinin Tarihsel Gelişimi
Kervaire değişmezi, ilk olarak Michel Kervaire tarafından 1960 yılında ortaya atılmıştır. Kervaire, bu değişmezi kullanarak, topolojik manifoldların sınıflandırılmasına önemli katkılar sağlamıştır. O zamandan beri, Kervaire değişmezi matematikçilerin ilgisini çekmiş ve üzerinde yoğun araştırmalar yapılmıştır.
İlk Bulgular
Kervaire değişmezi ile ilgili ilk bulgular, düşük boyutlarda elde edilmiştir. 2. boyutta değişmezin değeri 1 olarak bulunmuştur. Daha sonra, 6 ve 14. boyutlarda da aynı sonuç elde edilmiştir. Bu bulgular, Kervaire değişmezinin topolojik uzayların sınıflandırılmasında önemli bir rol oynadığını göstermiştir.
Daha Yüksek Boyutlar
Daha yüksek boyutlarda Kervaire değişmezinin değerini belirlemek, daha karmaşık ve zorlu bir problemdir. 30 ve 62. boyutlarda yapılan çalışmalar, bu boyutlarda da değişmezin değerinin 1 olduğunu göstermiştir. Ancak, daha yüksek boyutlarda durumun nasıl olduğu uzun süre belirsiz kalmıştır.
Çalışmanın Yöntemi ve Zorlukları
Çinli bilim insanlarının başarısının arkasında, titiz bir çalışma ve modern teknolojinin kullanımı yatmaktadır. Geleneksel matematiksel yöntemlerin yanı sıra, bilgisayar sistemlerinden de yararlanarak büyük miktarda veriyi analiz etmişler ve karmaşık hesaplamaları gerçekleştirmişlerdir.
Bilgisayar Destekli Hesaplamalar
Kervaire değişmezi probleminin çözümü, büyük ölçüde bilgisayar destekli hesaplamalara dayanmaktadır. Bilim insanları, özel algoritmalar geliştirerek ve yüksek performanslı bilgisayarlar kullanarak, 126. boyutta Kervaire değişmezinin değerini belirlemeyi başarmışlardır. Bu, matematiksel araştırmalarda bilgisayar teknolojisinin giderek daha önemli bir rol oynadığını göstermektedir.
Olasılıkların İncelenmesi
126. boyutta Kervaire değişmezinin değerini belirlemek için, bilim insanları 105 farklı olasılığı tek tek incelemek zorunda kalmışlardır. Bu, son derece zaman alıcı ve zorlu bir süreçtir. Ancak, titiz bir çalışma ve sistematik bir yaklaşımla, tüm olasılıkları eleyerek doğru sonuca ulaşmayı başarmışlardır.
Hakem Değerlendirme Süreci
Çinli bilim insanlarının çalışması henüz hakem değerlendirme sürecinden geçmemiştir. Bu süreç, bilimsel araştırmaların doğruluğunu ve güvenilirliğini sağlamak için önemli bir adımdır. Hakemler, çalışmanın yöntemini, sonuçlarını ve yorumlarını detaylı bir şekilde inceleyerek, çalışmanın bilimsel standartlara uygun olup olmadığını değerlendirirler.
Hakem Onayının Önemi
Hakem onayı, bir bilimsel çalışmanın güvenilirliğini ve kabul edilebilirliğini artırır. Onaylanan çalışmalar, genellikle saygın bilimsel dergilerde yayınlanır ve geniş bir kitleye ulaşır. Kervaire değişmezi ile ilgili bu çalışmanın hakem onayı alması, matematik dünyasında büyük bir gelişme olarak kabul edilecektir.
Çalışmanın Potansiyel Etkileri
Çinli bilim insanlarının başarısı, matematik dünyasında heyecan yaratmasının yanı sıra, gelecekteki araştırmalar için de önemli bir ilham kaynağı olabilir. Kervaire değişmezi probleminin çözümünde kullanılan tekniklerin, diğer çözülememiş matematiksel problemlerin çözümünde de kullanılabileceği düşünülmektedir.
Yeni Tekniklerin Geliştirilmesi
Kervaire değişmezi probleminin çözümü, yeni matematiksel tekniklerin geliştirilmesine yol açabilir. Bilim insanları, bu teknikleri kullanarak, topoloji, geometri ve cebir gibi farklı alanlardaki problemleri çözmeyi deneyebilirler. Bu, matematiğin genel olarak ilerlemesine katkı sağlayabilir.
Diğer Problemlere Uygulanabilirlik
Kervaire değişmezi probleminin çözümünde kullanılan yöntemlerin, diğer çözülememiş problemlere uygulanabilirliği, matematik dünyasında büyük bir merak uyandırmaktadır. Eğer bu mümkün olursa, matematik alanında önemli bir devrim yaşanabilir ve birçok zorlu problem çözülebilir.
Kervaire Değişmezinin Uygulama Alanları
Kervaire değişmezi, teorik bir kavram olmasına rağmen, matematik ve fizik alanlarında çeşitli uygulama alanlarına sahiptir. Özellikle, topolojik uzayların sınıflandırılması, sicim teorisi ve kuantum alan teorisi gibi alanlarda önemli bir rol oynamaktadır.
Topolojik Uzayların Sınıflandırılması
Kervaire değişmezi, topolojik uzayların sınıflandırılmasında kullanılan önemli bir araçtır. Bu değişmez, farklı topolojik uzayları birbirinden ayırt etmeye ve onların özelliklerini anlamaya yardımcı olur. Bu, matematiğin temel problemlerinden biri olan topolojik uzayların sınıflandırılması konusunda önemli bir adımdır.
Sicim Teorisi
Sicim teorisi, evrenin temel yapı taşlarının nokta parçacıklar yerine sicimler olduğu bir fizik teorisidir. Kervaire değişmezi, sicim teorisinde ortaya çıkan bazı matematiksel problemlerin çözümünde kullanılabilir. Bu, matematiğin fizik alanındaki uygulamalarına bir örnektir.
Kuantum Alan Teorisi
Kuantum alan teorisi, parçacıkların ve alanların kuantum mekaniksel davranışlarını inceleyen bir fizik teorisidir. Kervaire değişmezi, kuantum alan teorisinde ortaya çıkan bazı matematiksel yapıların anlaşılmasına yardımcı olabilir. Bu, matematiğin teorik fizik alanındaki önemini vurgulamaktadır.
Matematikte Gelecek Trendler
Kervaire değişmezi probleminin çözümü, matematikteki gelecek trendler hakkında da önemli ipuçları vermektedir. Bilgisayar destekli hesaplamaların ve yeni matematiksel tekniklerin geliştirilmesi, gelecekteki araştırmaların yönünü belirleyebilir.
Bilgisayar Destekli Matematik
Bilgisayar destekli matematik, matematiksel problemlerin çözümünde bilgisayar teknolojisinin kullanılmasını içerir. Bu yaklaşım, büyük miktarda verinin analiz edilmesine, karmaşık hesaplamaların yapılmasına ve yeni matematiksel modellerin geliştirilmesine olanak tanır. Kervaire değişmezi probleminin çözümü, bilgisayar destekli matematiğin gücünü göstermektedir.
Yeni Matematiksel Teknikler
Kervaire değişmezi probleminin çözümü, yeni matematiksel tekniklerin geliştirilmesine yol açabilir. Bu teknikler, topoloji, geometri, cebir ve analiz gibi farklı alanlardaki problemleri çözmek için kullanılabilir. Bu, matematiğin genel olarak ilerlemesine katkı sağlayabilir.
Sonuç
Kervaire değişmezi probleminin çözümü, matematik dünyasında önemli bir dönüm noktasıdır. Çinli bilim insanlarının bu alanda gerçekleştirdiği çığır açan çalışma, matematik camiasında büyük bir heyecan yaratmış durumda. Hakem değerlendirme sürecinin tamamlanmasıyla birlikte, bu keşfin matematik alanında yeni ufuklar açması bekleniyor. Bu başarı, matematiksel araştırmalarda bilgisayar teknolojisinin giderek daha önemli bir rol oynadığını göstermekte ve gelecekteki araştırmalar için önemli bir ilham kaynağı olmaktadır.
| Boyut | Kervaire Değişmezi Değeri | Bulunduğu Yıl |
|---|---|---|
| 2 | 1 | Bilinmiyor |
| 6 | 1 | 1964 |
| 14 | 1 | 1964 |
| 30 | 1 | 1984 |
| 62 | 1 | 1984 |
| 126 | 1 | 2024 (Beklemede) |
“`





